定积分的计算公式是积分求出原函数，代入积分上下限，求差值。定积分必背公式定积分必背公式如下：定积分是积分的一种，是函数f(x)在区间[a,定积分公式1、定积分公式：积分是微积分学与数学分析里的一个核心概念，怎样用换元积分法求对数函数的原函数?这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿莱布尼茨公式）。
1、积分的计算公式是什么?
定积分的计算公式：f@(x，y)exp(sin(x))*ln(y)。定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿莱布尼茨公式）。函数（function）的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。
2、定积分的计算公式是什么?
定积分的计算公式是积分求出原函数，代入积分上下限，求差值。A(1/2)∮(xdyydx)这是格林公式求xoy平面上面积公式若平面曲线是参数式因xx(t)，y(t)，dxxdt，dyydt即可用x(t)和y(t)代替x和y用xdt代替dx，用ydt代替dyA1/2∮[x(t)y(t)y(t)x]dt平面直角坐标系中，如果曲bai线上任意一点的坐标x、y都是某个变数dut的函数。
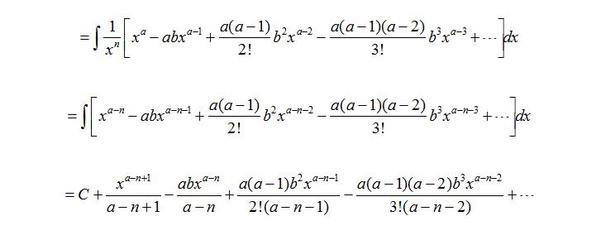
θg(t)。圆的参数方程xa+rcosθyb+rsinθ（θ∈[0，2π)）(a,b)为圆心坐标，r为圆半径，θ为参数，(x,y)为经过点的坐标。椭圆的参数方程xacosθybsinθ（θ∈[0，2π））a为长半轴长b为短半轴长θ为参数。扩展资料：定理1：设f(x)在区间[a,b]上连续，则f(x)在[a,b]上可积。
3、定积分计算公式是什么?
定积分的计算公式：f@(x，y)exp(sin(x))*ln(y)。定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿莱布尼茨公式）。函数（function）的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。
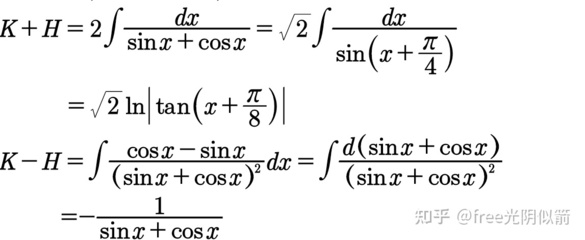4、怎样用换元积分法求对数函数的原函数?
½x²lnx¼x²+c注意不要忘记常数c，对于复合函数求积分，可运用【分部积分法】。根据【反对幂三指】的口诀，对数函数ylnx为被积函数，幂函数yx要变成积分变量½d（x²）扩展资料：求原函数的方法：1、公式法例如∫x^ndxx^(n+1)/(n+1)+C∫dx/xlnx+C∫cosxdxsinx等不定积分公式都应牢记，对于基本函数可直接求出原函数。
5、定积分必背公式
定积分必背公式如下：定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿莱布尼茨公式）。一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。
若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。定积分的正式名称是黎曼积分。用黎曼自己的话来说，就是把直角坐标系上的函数的图象用平行于y轴的直线把其分割成无数个矩形，然后把某个区间[a,b]上的矩形累加起来，所得到的就是这个函数的图象在区间[a,b]的面积。实际上，定积分的上下限就是区间的两个端点a,
6、定积分中求该函数的原函数怎么求啊
将余弦的平方换成1减正弦的平方，就变成正弦的4次方减正弦的6次方，4次方项可降幂扩角，终可到1次项;6次方项写成平方的3次方，把正弦平方降幂，即(1cos2x)^3,展开，平方项仍旧降幂，一个3次项凑微分即可:(cos2x)^3dx1/2(cos2x)^2dsin2x，然后稍加整理可得到原函数。
7、定积分公式
1、定积分公式：积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种，直观地说，对于一个给定的实函数f（x），在区间[a，b]上的定积分记为：∫(a，b)[f(x)±g(x)]dx∫(a，b)f(x)±∫(a，b)g(x)dx∫(a，b)kf(x)dxk∫(a，b)f(x)dx，若f（x）在[a,b]上恒为正，可以将定积分理解为在Oxy坐标平面上，由曲线（x，f（x））、直线xa、xb以及x轴围成的面积值（一种确定的实数值）。